Tal teoria ficou conhecida também como “teoria ingênua” ou “teoria intuitiva” por causa da descoberta de várias antinomias (ou paradoxos) associados à idéia central da própria teoria. Tais antinomias levaram a uma axiomatização das teorias matemáticas futuras, influenciando de modo indelével as ciências da matemática e da lógica.
Mais tarde, a teoria original receberia complementos e aperfeiçoamentos no início do século XX por outros matemáticos.
O conhecimento prévio de tal teoria serve como base para o desenvolvimento de outros temas na matemática, como relações, funções, análise combinatória, probabilidade, etc.
Como definição intuitiva de conjuntos, dadas por Cantor, surgiam em sua teoria exemplos como:
- um conjunto unitário possui um único elemento
- dois conjuntos são iguais se possuem exatamente os mesmos elementos.
- conjunto vazio é o conjunto que não possui nenhum elemento
- Os conjuntos podem ser finitos ou infinitos. Um conjunto finito pode ser definido reunindo todos os seus elementos separados por vírgulas. Já um conjunto infinito pode ser definido por uma propriedade que deve ser satisfeita por todos os seus membros.
A idéia de conjunto era um conceito primitivo e auto explicativo de acordo com a teoria; não necessitaria de definição.
Esta forma de representar um conjunto, pela enumeração de seus elementos é denominada “forma de listagem”. Poderia-se representar o mesmo conjunto por uma determinada propriedade de seus elementos, sendo x, por exemplo, um número qualquer do conjunto Z representado abaixo:
Z = {1,3,5,7,9,11, … }
teríamos, concluindo:
Z = { x | x é ímpar e positivo } = { 1,3,5, … }.
Merece destaque outras relações básicas, que independem de um cálculo matemático mais complexo, utilizando-se lógica básica e pura.
São exemplos desta afirmação as relações a seguir:
1 – Pertinência
Estabelece se um elemento pertence ou não pertence a um conjunto pré-estabelecido:
- dado um número x, caso ele pertença ao conjunto, escrevemos x Є A, ou “x” pertence ao conjunto A
- caso “x” não pertença ao conjunto, registra-se x Є A.
- um conjunto sem elementos é um conjunto vazio, representado pela letra grega φ (phi).
2 – Subconjunto
Caso todo o elemento do conjunto A pertença também ao conjunto B, sem que todos os elementos deste segundo grupo pertençam todos a B, diremos que “A é subconjunto de B”: A c B
3 – Conjuntos numéricos fundamentais
Trata-se de qualquer conjunto cujos elementos são números, entre eles, o conjunto de números naturais N = {0,1,2,3,4,5,6…}; o conjunto de números inteiros Z = {…, -4,-3,-2,-1,0,1,2,3,… } (sendo que N с Z); conjunto de números racionais Q = { 2/3, -3/7, 0,001, 0,75, 3, etc.) (sendo que N с Z с Q); conjunto de números irracionais, etc.
Ocorre união quando o conjunto união contempla todos os elementos de dado conjunto A ou de dado conjunto B.
Exemplo: {0,1,3} U { 3,4,5 } = { 0,1,3,4,5}.
Assim, através de suas numerosas combinações, que fornecem poderosa ferramenta para a construção da matemática de base axiomática, apesar de seu conteúdo predominantemente dedutivo, logo surgiu o “Paradoxo de Russel”, que é a contradição mais famosa da teoria dos conjuntos.
5 - Intersecção de conjuntos
Dados os conjuntos A e B, define-se como intersecção dos conjuntos A e B ao conjunto representado por 
, formado por todos os elementos pertencentes a A e B, simultaneamente, ou seja:
Quando queremos a intersecção de dois conjuntos é o mesmo que dizer que queremos os elementos que eles têm em comum.
Exemplo: Dado dois conjuntos A = {1, 2, 3, 4, 5, 6} e B = {5, 6, 7}, a intersecção é representada pelo símbolo ∩, então:
A ∩ B = {5, 6},pois 5 e 6 são elementos que pertencem aos dois conjuntos. Se dois conjuntos não tem nenhum elemento comum a intersecção deles será um conjunto vazio.
Dentro da interseção de conjuntos há algumas propriedades:
1) A intersecção de um conjunto por ele mesmo é o próprio conjunto: A ∩ A = A
2) A propriedade comutatividade na intersecção de dois conjuntos é: A ∩ B = B ∩ A.
3) A propriedade associativa na intersecção de conjuntos é: A ∩ (B ∩ C) = (A ∩ B) ∩ C.
6 - Diferença entre conjunto
Dados os conjuntos A e B, define-se como diferença entre A e B (nesta ordem) ao conjunto representado por A-B, formado por todos os elementos pertencentes a A, mas que não pertencem a B, ou seja:
Então A - B serão os elementos do conjunto A menos os elementos que pertencerem ao conjunto B.
Portanto:
A - B = {0, 1, 2, 3, 4}.
7 - Conjunto complementar
Conjunto complementar está relacionado com a diferença de conjunto.
Exemplo:
A = {2, 3, 5, 6, 8}
B = {6,8}
B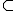 
A, então o conjunto complementar será CAB = A - B = {2, 3, 5}.
8 - Conjunto das Partes
Dado um conjunto A com um número finito de elementos, dizemos que o conjunto das partes de A é aquele formado por todos os subconjuntos de A. Denotamos o conjunto das partes de A por P(A).
Ex.: A={a, b, c}, P(A)={ Æ, {a}, {b}, {c}, {a, b}, {a, c},{b, c},{a, b, c}}
Atenção: Lembre-se que dentre os subconjuntos de um dado conjunto, estão o conjunto vazio e o próprio conjunto.
Ex.: Seja B = {a, e, i}, encontre P(B).
9 - Igualdade de Conjuntos
Dois ou mais conjuntos são iguais quando apresentam os mesmos elementos, em qualquer ordem, sendo que elementos iguais, num mesmo conjunto, serão considerados uma única vez.
Daí, podemos afirmar que é verdadeira a igualdade dada por: A= { a; b; c} = { c; b; a} = { a; a; a; b; b; b; c; c}
Simbolicamente a igualdade entre conjuntos fica definida como:
10 - Produto Cartesiano:
Dados os conjuntos A e B, chama-se produto cartesiano A com B, ao conjunto A x B, formado por todos os pares ordenados (x,y), onde x é elemento de A e y é elemento de B, ou seja:
11 - Número de subconjuntos de um conjunto:
Se um conjunto A possuir n elementos, então existirão 2n subconjuntos de A.