FUNÇÃO EXPONENCIAL

Toda relação de dependência, em que uma incógnita depende do valor da outra, é denominada função. A função denominada como exponencial possui essa relação de dependência e sua principal característica é que a parte variável representada por x se encontra no expoente.

Observe:

y = 2 ^x
y = 3 ^{x + 4}
y = 0,5 ^x
y = 4^x

A lei de formação de uma função exponencial indica que a base elevada ao expoente x precisa ser maior que zero e diferente de um, conforme a seguinte notação:

onde o número b é denominado base. A figura abaixo mostra os gráficos das funções f(x) = 2^xe g(x) = 10^x.

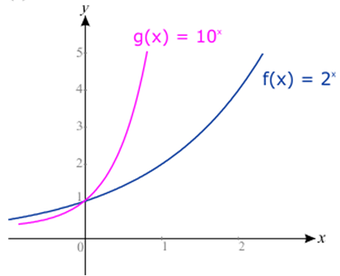
Funções exponenciais são geralmente utilizadas para representar o crescimento (decrescimento) de uma quantidade ou de uma população.

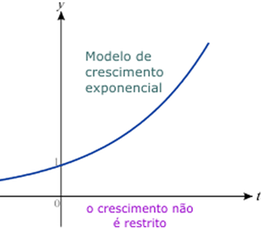
Observe que:

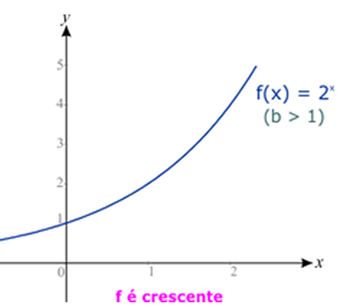
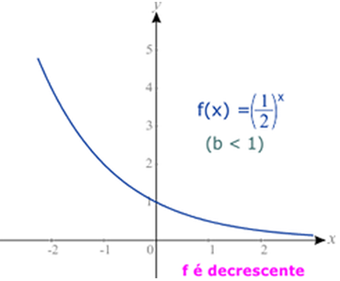
Assim como todas as funções do tipo f(x) = b^x, são funções passam pelo ponto (0,1).

Funções exponenciais são sempre positivas: b^x > 0

é crescente se b > 1 e decrescente se 0 < b < 1.

O domínio de f(x) = b^x é o conjunto de todos os números reais.

A imagem de f(x) = b^x é o conjunto de todos os números reais positivos -]0,+[.

Quanto maior for a base da função f(x) = b^x, mais inclinado é o seu gráfico.

A função f(x) = e^x, cuja base é a constante de Euler e (), desempenha um papel muito importante nas aplicações e será referida como a função exponencial.