ℝ é fechado em relação à adição, subtração, multiplicação e divisão por números reais diferentes de zero.
O conjunto dos números reais é denso, isto é, há infinitos reais entre dois reais quaisquer e, da mesma forma que o conjunto dos irracionais, não é enumerável.
Vejamos, então, as propriedades válidas em ℝ.
1. Adição e multiplicação
Associativa
Podemos associar, de formas diferentes, quaisquer números reais a, b e c:
(a + b) + c = a + (b + c)
(a · b) · c = a · (b · c)
Comutativa
A ordem das parcelas não altera a soma ou a ordem dos fatores não altera o produto, para quaisquer números reais a e b:
a + b = b + a a · b = b · a
Elemento neutro
Zero é o elemento neutro da adição, para qualquer número real a.
a + 0 = 0 + a = a
Um é o elemento neutro da multiplicação, para qualquer número real a.
a · 1 = 1 · a = a
Elemento oposto
Qualquer que seja o valor do número real a, existe um número real -a, tal que:
a + (- a) = 0 e (- a) + a = 0
Elemento inverso
Qualquer que seja o número real a, a ≠0
Distributiva
Quaisquer que sejam a, b e c, temos:
a · (b + c) = a · b + a · c
(b + c) · a = b · a + c · a
Exemplo:
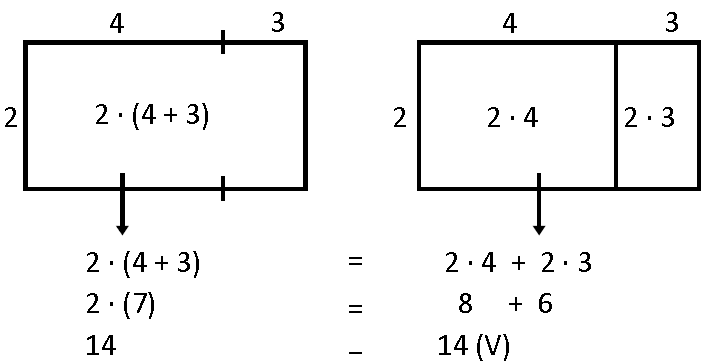
A área dos retângulos abaixo ilustra a propriedade distributiva.