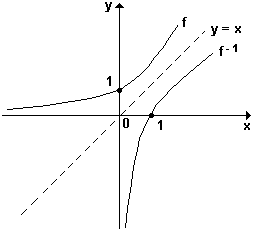Definindo função inversa, se f é uma função bijetora assim para cada x tem-se um y correspondente, assim a inversa de f é a função f-1 que define que para cada y teremos um correspondente x.
Regra prática: Sendo uma função bijetora f(x) = y teremos que a inversa de f, que será representada por f-1, será f(y) = x, ou seja f-1(x) = y.
Exemplo prático: Seja uma função bijetora f(x) = 3x + 6, teremos que a inversa de f(x), ou seja f-1(x), será , pois y = 3x + 6 → para a inversa x = 3y + 6 , então
.
Calcular f(3) temos f(3) = 3.3 + 6 = 12.
Agora ao calcularmos f-1(12) = 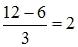 .
.
Assim percebe-se a relação entre a função e a sua inversa.