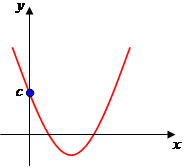
Denominamos função do segundo grau a qualquer função f: R→R, tal que: f(x) = ax² + bx + c (com ≠ 0).

Os gráficos das funções do 2° grau são sempre parábolas.

O que é exatamente uma parábola?

As parábolas são curvas especiais construídas de uma tal maneira que cada um dos infinitos pontos que formam a parábola ficam à mesma distância de uma certa reta (reta diretriz da parábola) e de um certo ponto (foco da parábola) que está fora da reta diretriz.

Na função f(x) = ax² + bx + c, o valor ∆ = b² - 4ac é chamado discriminante da expressão quadrática.

Para construir o gráfico da função y= x², como na função do 1º grau, basta atribuir valores reais para x para obtermos seus valores correspondentes para y.

x y=f(x)=x² 2 4 -1 1 0 0 1 1 2 4 3 9

 

VÉRTICE DA PARÁBOLA

O vértice de uma parábola é um ponto da parábola com várias características interessantes.

Ele será o ponto mais alto (ponto de máximo) ou o ponto mais baixo (ponto de mínimo) da parábola.

Além disto, o vértice da parábola divide a parábola em duas partes, sendo uma crescente e outra decrescente.

 

COORDENADAS DO VÉRTICE

Entende-se por vértice, o ponto onde o traçado do gráfico muda de direção, ou seja, onde ele deixa de ser decrescente e passa a ser crescente ou vice-versa. A coordenada x do vértice da parábola pode ser determinada por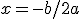

Exemplo: Determine as coordenada do vértice da parábola y= x² - 4x + 3

Temos: a=1, b=-4 e c=3

 

Logo, a coordenada x será igual a 2, mas e a coordenada y?

Simples: Vamos substituir o valor obtido da coordenada x e determinar o valor da coordenada y.

Assim, para determinarmos a coordenada y da parábola y=x² - 4x + 3, devemos substituir o valor de x por 2.

y = (2)² - 4.(2) + 3 = 4 - 8 + 3 = -1

 

Logo, as coordenadas do vértice serão V=(2,-1)

Portanto, para determinarmos as coordenadas do vértice de uma parábola, achamos o valor da coordenada x (através de x=-b/2a) e substituindo este valor na função, achamos a coordenada y!

O ZERO DA FUNÇÃO

Como determinar a raiz ou zero da função do 2º grau?

Para a resolução desta é necessário recorremos à fórmula de Bháskara, qual seja:

 

Exemplo: Determine a raiz da função y=x² + 5x + 6.

Fazendo y=f(x)=0,

temos x² + 5x + 6 = 0

Aplicando a fórmula descrita acima acha-se dois resultados:

Um resultado considerando o sinal positivo da raiz e o outro considerando-a como negativa.

Assim, acharemos que x = -2 e x` = -3.

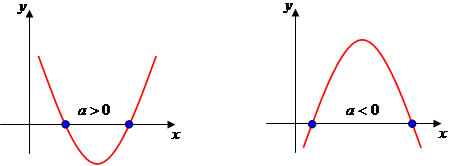
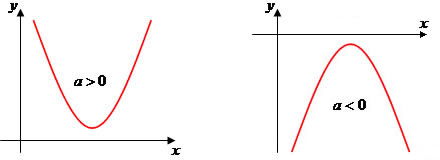
CONCAVIDADE DA PARÁBOLA

(1) a>0 concavidade para cima

(2) a<0 concavidade para baixo

Condições

∆ > 0, a parábola intercepta o eixo das abscissas em dois pontos.

∆ = 0, a parábola intercepta o eixo das abscissas somente em um ponto.

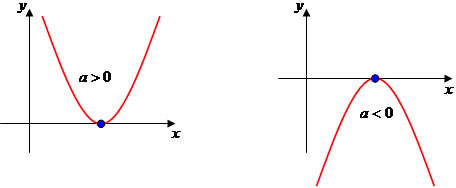
∆ < 0, a parábola não intercepta o eixo das abscissas. 

Outra relação importante na função do 2º grau é o ponto onde a parábola corta o eixo y. Verifica-se que o valor do coeficiente c na lei de formação da função corresponde ao valor do eixo y onde a parábola o intersecta.