Estudo do sinal Estudar o sinal de uma função f(x) significa determinar para que valores de x ∈ ao domínio da função a imagem f(x) será positiva, negativa ou nula, ou seja f(x) > 0, f(x) < 0 ou f(x) = 0.
Existe um interesse especial no estudo de função em que y pode ser calculado a partir de x por meio de uma fórmula (ou regra, ou lei).
Exemplo 1:
A lei de correspondência que associa cada número real x ao número y o dobro de x, é uma função definida pela fórmula y = 2x, ou f(x) = 2x. O domínio e o conjunto imagem dessa função são R. A notação da função é, portanto, f: R ![]() R tal que f(x) = 2x.
R tal que f(x) = 2x.
Nessa função temos:
- Para x = 5, vem y = 2.5 = 10. Dizemos que f(5) = 10.
- A imagem de x = -3 é f(-3) = 2.(-3); f(-3) =-6.
- x = 11,5 corresponde a y = 2. (11,5) = 23.
Para fazermos o estudo dos sinais da função de 1º grau, precisamos antes estabelecer uma importante propriedade dessa função.
Uma função de 1º grau, f(x) = ax + b:
- é crescente se a > 0
- é decrescente se a < 0
F(x) = ax + b
Como fazer o estudo dos sinais de f(x) = ax + b
Por exemplo, para estudar os sinais de f(x) = -x + 5
1º) Cálculo da raiz: f(x) = 0 → -2x + 5 = 0 → x = 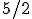
2º) Como a = -2, a função é decrescente. Portanto, o gráfico de f tem o seguinte aspecto:
Assim temos:
f(x) = 0 ↔ x = 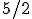
f(x) > 0 ↔ x < 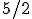
f(x) < 0 ↔ x > 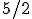
Domínio (D), contradomínio (CD), Imagem (Im).