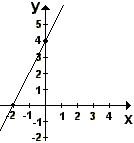Os quatro quadrantes em que um plano cartesiano fica dividido por seus dois eixos oferecem várias oportunidades de aplicar a idéia de transformações a desenhos de funções.
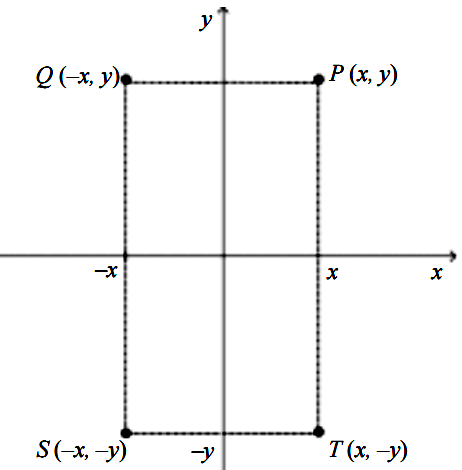
Para entender como funciona, vamos pensar em um ponto P representado por um par (x,y). Se os números x e y forem positivos não nulos, então o ponto está representado no primeiro quadrante.
O que ocorre se tomarmos o ponto Q representado pelo par (-x,y)?
O ponto terá a mesma ordenada y que o ponto P, mas vai ocupar o lugar simétrico ao ponto P em relação ao eixo y.
Se tomarmos o ponto T (x,-y), esse ponto é simétrico a P em relação ao eixo x. Já um ponto S (-x,-y) está no terceiro quadrante.
Ele pode ser obtido a partir de P por meio de uma rotação em torno da origem (0,0) e de ângulo 180°
que S pode também ser obtido a partir de P por duas sucessivas reflexões em relação aos eixos coordenados.
Veja a ilustração abaixo:
Toda função de 1º grau origina um gráfico. Este pode ser obtido atribuindo-se valores quaisquer para x e associando aos valores correspondentes para y.
Ex.: Apegando-se à função f(x)= 2x +4
Atribuindo-se valores, temos:
Quando x for 0, teremos que f(0)= 2.0 + 4 f(0)= 4
Logo, o primeiro ponto do gráfico é (0,4)
Se considerarmos o x como -2 agora, teremos que f(-2)= 2(-2) +4 F(-2)=0
Portanto, o segundo par é (-2,0)
|
X |
f(x) ou y |
|
0 |
4 |
|
-2 |
0 |
Para este procedimento basta calcular, como vimos, o valor de f(x), ou y, com quaisquer valores atribuídos para x.
Exemplo de aplicação da função de 1º grau.
1 - Na produção de peças, uma indústria tem um custo fixo de R$ 8,00 mais um custo variável de R$ 0,50 por unidade produzida. Sendo x o número de unidades produzidas:
a) escreva a lei da função que fornece o custo total de x peças.
b) calcule o custo de 100 peças.
Resolução:
a) Sabendo que R$8,00 é custo fixo, sabemos que este resultado deverá ser acrescido sempre, sem alterações.
Contudo, verificamos que R$0,50 é cobrado a cada unidade produzida, ou seja.
Logo façamos x como a quantidade de peças a serem produzidas e y o custo dessas. Então:
Preço = preço fixo + preço2
y = 8 + 0,50*x
*lembrando que o preço2 é composto de R$0,50 a cada peça produzida.
b) Como já sabemos a lei, agora é só substituir.
Como se deseja saber o custo de 100 peças, calculamos f(100)
f(100) = 8+0,50*100 = 58
ou seja, 8 peças custam R$58,00.