FUNÇÃO POLINOMIAL

Uma Função Polinomial é uma função dada por um polinômio, ou seja, para todo x pertencente ao domínio da função, encontramos o valor de y na imagem da função calculando o valor de um polinômio no valor de x do domínio.

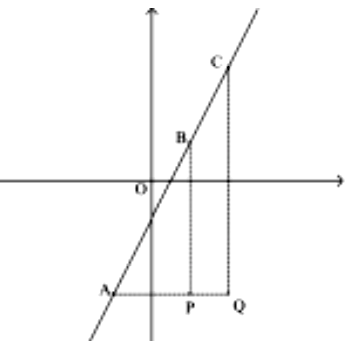
Uma função polinomial de primeiro grau é da forma y = ax + b, onde a e b são constantes, x é a variável independente, y é a variável dependente e a ≠ 0.

Observemos que, se a = 0, temos y = b, que é uma função constante.

O gráfico de y = b é uma reta horizontal, ou seja, uma reta paralela ao eixo das abscissas, pois para qualquer valor de x, o valor de y é sempre o mesmo: b. Nesse caso, a função y = b é uma função polinomial de grau zero.

Quando a ≠ 0, o gráfico de y = ax + b é uma reta não horizontal mas também não vertical - lembre que uma reta vertical não pode ser gráfico de uma função.

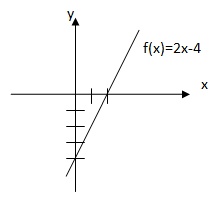
Exemplos:

Toda função do tipo y=m.x+b, que é polinômio de grau 1, tem por gráfico uma reta. A estas funções chamam-se funções afins.

Os exemplos mais importantes de funções polinomiais são:

A função constante, que é uma função polinomial de grau 0, f(x)=k, k constante, e que assume o mesmo valor k para todo x no domínio de f.

A função afim, f(x)=ax+b, a≠0, é uma função polinomial de grau 1 com b≠0.

No caso de b=0 então f(x)=ax ,e a função é dita linear, exemplo importantíssimo pois nesse caso, vale:

f(x+y)=a(x+y) = ax+ay = f(x)+f(y) → f(x+y) = f(x)+f(y), aditividade, e

f(kx)=a(kx) = k(ax)=k.f(x) → f(kx)=k.f(x) xDom f, homogeneidade.

Se a>0, então a função afim é crescente e se a<0 ela é decrescente.

Vamos dar um exemplo:

Seja f(x)=2x-4 , função afim crescente. Para fazer seu gráfico basta obter dois pontos. Podemos escolher os pontos, vamos tomar x=0 e x=2. Então f(0)=-4 e f(2)=0,assim o gráfico de f representa uma reta que passa pelos pontos (0; -4) e (2; 0) no plano cartesiano, como abaixo:

Outro exemplo de grande utilidade e importância de função polinomial é a função quadrática f(x)=ax^2+b^x+c, a≠0, que tem grau 2, cujo gráfico é uma parábola.