Conceito
A trigonometria, palavra formada por três radicais gregos: tri (três), gonos (ângulos) e metron (medir), têm por objetivo o cálculo das medidas dos lados e ângulos de um triângulo.
TRIGONOMETRIA
A trigonometria teve seu início na antiguidade remota, quando se acreditava que os planetas descreviam órbitas circulares em torno da Terra, surgindo daí o interesse em relacionar o comprimento da corda de uma circunferência com o ângulo central por ela subtendido.
Medir distâncias é uma necessidade antiga da humanidade, facilmente atendida no caso de envolver pontos próximos. Basta verificar quantas vezes uma dada unidade de medida está contida no comprimento a ser medido. Este é o princípio dos instrumentos mais comuns para medir comprimentos: réguas, fitas métricas, trenas, etc.
Por que estudar Trigonometria?
Há situações, em que se deseja efetuar medidas envolvendo objetos que não são diretamente acessíveis. Atualmente, a trigonometria não se limita apenas a estudar os triângulos. Sua aplicação se estende a outros campos da Matemática, como análise, e a outros campos da atividade humana, como a Eletricidade, a Mecânica, a Acústica, a Música, a Topologia, a Engenharia Civil etc.
Observem algumas situações:
- Você já parou para imaginar como os navegadores da antiguidade faziam para calcular a que distância da terra eles encontravam-se enquanto navegavam?
- Seria impossível medir a distância da Terra à Lua, porém com a trigonometria se torna simples.
- Um engenheiro precisa saber a largura de um rio para construir uma ponte, o trabalho dele é mais fácil quando ele usa dos recursos trigonométricos.
- Um cartógrafo (desenhista de mapas) precisa saber a altura de uma montanha, o comprimento de um rio, etc. Sem a trigonometria ele demoraria anos para desenhar um mapa.
Pode-se dizer que foi a Astronomia a grande impulsionadora da Trigonometria, pois foi o astrônomo grego Hiparco (190 a.C - 125 a.C) quem empregou pela primeira vez relações entre os lados e os ângulos de um triângulo retângulo.
Na Grécia antiga, entre os anos de 190 a.C. e 125 a.C., viveu Hiparco, um matemático que construiu a primeira tabela trigonométrica. Esse trabalho foi muito importante para o desenvolvimento da Astronomia, pois facilitava o cálculo de distâncias inacessíveis, o que lhe valeu o título de PAI DA TRIGONOMETRIA.
Astrolábio - Um dos mais antigos instrumentos científicos, que teria surgido no século III a.C. A sua invenção é atribuída ao matemático e astrônomo grego Hiparco.
O objeto inicial da Trigonometria era o tradicional problema da resolução de triângulos, que consiste em determinar os seis elementos dessa figura (três lados e três ângulos) quando se conhecem três deles, sendo pelo menos um deles um lado.
Razões trigonométricas no triângulo retângulo
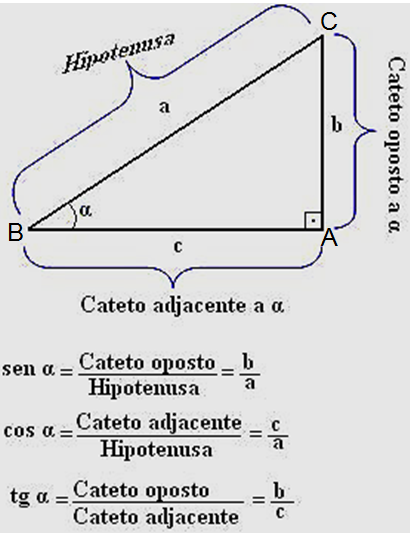
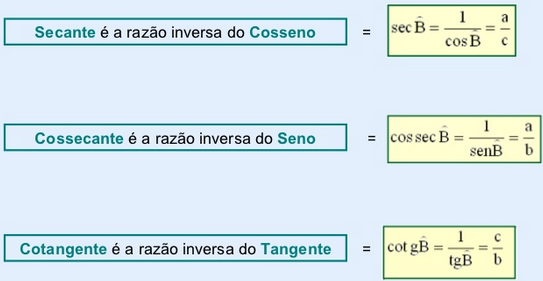
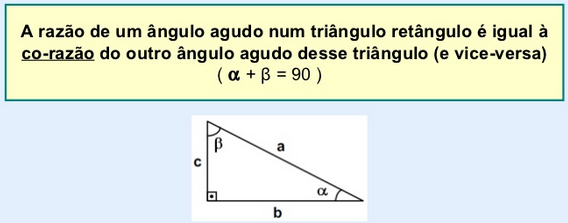
Ao tomarmos um ângulo agudo como referência de um triângulo retângulo, as razões podem ser chamadas por nomes especiais.
São eles:
- seno,
- cosseno e
- tangente.
Tomando o ângulo A como referência no triângulo ABC, temos que:
Ângulos Arbitrários
