É frequente o uso de expressões que refletem acréscimos ou reduções em preços, números ou quantidades, sempre tomando por base 100 unidades.

Alguns exemplos:

• A gasolina teve um aumento de 15%
  Significa que em cada R$100 houve um acréscimo de R$15,00
• O cliente recebeu um desconto de 10% em todas as mercadorias.
  Significa que em cada R$100 foi dado um desconto de R$10,00

Dos jogadores que jogam no Grêmio, 90% são craques.
Significa que em cada 100 jogadores que jogam no Grêmio, 90 são craques.
 

Toda a razão que tem para consequente o número 100 denomina-se razão centesimal.

Alguns exemplos:

 

Podemos representar uma razão centesimal de outras formas:

As expressões 7%, 16% e 125% são chamadas taxas centesimais ou taxas percentuais.

Considere o seguinte problema:

João vendeu 50% dos seus 50 cavalos. Quantos cavalos ele vendeu?
Para solucionar esse problema devemos aplicar a taxa percentual (50%) sobre o total de cavalos.

Logo, ele vendeu 25 cavalos, que representa a porcentagem procurada.

Sua utilização está tão disseminada que a encontramos nos meios de comunicação, nas estatísticas, em máquinas de calcular, etc. A utilização da porcentagem se faz por regra de 3 simples.

Por exemplo, a vendedora de uma loja ganha 3% de comissão sobre as vendas que faz. Se as vendas do mês de outubro forem de R$ 3.500,00 qual será sua comissão?

Equacionando e montando a regra de 3 temos:

Na regra de 3, quando as grandezas são diretamente proporcionais (no caso, quanto maior a venda, maior a comissão) usamos setas paralelas e multiplicamos os termos em cruz, como se vê abaixo:

Ora, se 100 x = 3500 x 3, então

Logo, a comissão será de R$ 105,00.

Existe outra maneira de encarar a porcentagem, que seria usar diretamente a definição:

3% = 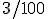, logo 3% de R$ 3.500,00 seriam 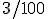x R$ 3.500,00 = R$ 105,00.

Em conversa com um amigo, ele me diz: O meu aluguel subiu R$ 200,00.

Para avaliarmos se o aumento foi grande ou pequeno, é preciso compararmos o acréscimo com o valor anterior do aluguel. Isto pode ser feito analisando o quociente entre os dois valores.

Assim, se o valor do aluguel era R$ 1.000,00 esta razão é 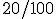, que costumeiramente analisamos deixando o denominador da fração igual a 100. Desta forma:

Interpretamos a razão p/100 dizendo que se o aluguel fosse R$ 100,00, o aumento teria sido de R$ 20,00.

 

Forma decimal

É comum representarmos uma porcentagem na forma decimal, por exemplo, 75% na forma decimal seria representado por 0,75.

Cálculo de uma porcentagem

Para calcularmos uma porcentagem p% de V, basta multiplicarmos a fração por V.

p% de V = X V

Assim temos:

1. 4% de 32 = 0,04 . 32 = 1,28
2. 15% de 180 = 0,15 . 180 = 27
3. 18% de 150 = 0,18 . 150 = 27
4. 35% de 126 = 0,35 . 126 = 44,1
5. 100% de 715 = 1,00 . 715 = 715
6. 115% de 60 = 1,15 . 60 = 69
7. 200% de 48 = 2,00 . 48 = 96

Todo o cálculo de porcentagem, como informado, é baseado no número 100.

 

O cálculo de tantos por cento de uma expressão matemática ou de um problema a ser resolvido é indicado pelo símbolo (%), e pode ser feito, na soma, por meio de uma proporção simples.

Para que se possam fazer cálculos com porcentagem (%), temos que fixar o seguinte: A taxa está para porcentagem (acréscimo, desconto, etc), assim como o valor 100 está para a quantia a ser encontrada.

Exemplo:

1) Efetue o cálculo 10% de 50

100% ___ 50

10% ___ X

100X = 500

X= 5

 

2) Efetua-se o resgate de um cheque pré-datado no valor de R$ 150,00 e obtém-se um desconto de 20%

100% ___ R$ 150,00

20% ___ X

X = R$ 30,00

 

Obs.: O cálculo de porcentagem pode ser feito da maneira apresentada anteriormente, ou poderá ser executada como uma multiplicação de fração, como no exemplo abaixo.

Nesse caso, lembre-se que multiplica-se sempre numerador com numerador e denominador com denominador.

10% = 10/100

34% = 34/100

 

3) Um jogador de basquete, ao longo do campeonato, fez 250 pontos, deste total 10% foram de cestas de 02 pontos. Quantas cestas de 02 pontos o jogador fez do total de 250 pontos.

10% de 250 = 10/100 . 250 = 2500/100 = 25

Portanto, do total de 250 pontos o jogador fez 25 pontos de 02 pontos.