Denominamos combinações simples de n elementos distintos tomados k a k (taxa k) aos subconjuntos formados por k elementos distintos escolhidos entre os n elementos dados. Observe que duas combinações são diferentes quando possuem elementos distintos, não importando a ordem em que os elementos são colocados.

Exemplo: No conjunto E= {a,b.c,d} podemos considerar:

a) combinações de taxa 2: ab, ac, ad,bc,bd, cd.

b) combinações de taxa 3: abc, abd,acd,bcd.

c) combinações de taxa 4: abcd.

Representando por Cm,p o número total de combinações de m elementos tomados p a p (taxa p) , temos a seguinte fórmula:

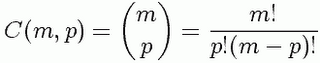
Nota: o número acima é também conhecido como Número binomial.

 

Exemplo: Uma prova consta de 15 questões das quais o aluno deve resolver 10. De quantas formas ele poderá escolher as 10 questões?

Solução:

Observe que a ordem das questões não muda o teste. Logo, podemos concluir que trata-se de um problema de combinação de 15 elementos com taxa 10.

Aplicando simplesmente a fórmula chegaremos a:

 

Exercício resolvido:
Um salão tem 6 portas. De quantos modos distintos esse salão pode estar aberto?

Solução:
Para a primeira porta temos duas opções: aberta ou fechada.
Para a segunda porta temos também, duas opções, e assim sucessivamente.
Para as seis portas, teremos então, pelo Princípio Fundamental da Contagem - PFC: